This is a backdated post, written more recently than the date claims, in order to give the impression that this blog has History. This is a dirty trick, but a necessary one, and I know that you, gentle reader, will keep my secret safe.
I have a feeling that, in some sense, someone in my position (a position which you, my noble blog adventurer, are likely to learn more of in time) should have on record a position on the Bayesian Issue. I will start this by dedicating a post to explaining The Bayesian Issue, and then later on having a post on where I stand on it.
The Bayesian Issue
The issue at hand is that of figuring out what is like to be true, given what we know and what we have assumed, a task that I can assume we all have some vested interest in. In quantitative science, the way we do this is to collect some data that we believe we be informative on the matter, combine this with some prior information or other assumptions, and use statistical inference to try and tease and answer from the data.
By way of example, if we suspect that a particular gene has a role in the immune system, we may breed up a number of mice that lack this gene, and count how many of them become infected with a disease of our choosing (maybe a Mycoplasma, everyone loves Mycoplasma). If more mice become infected than we would expect from healthy mice*, we have evidence that the gene is immune-related. But how do we know enough mice have fallen ill for us to rule out random chance, the mice we procured happening to be more sickly than your average rodent?

One way we could phrase this problem would be to say ‘what is the chance of seeing at least this many sick mice if the gene had no effect’, with the idea that if the knockout mice are especially sickly, we would see more sick mice than we’d expect from a batch of normal mice (we can use the Binomial Distribution, given that normal mice has a probability p of getting ill). This approach is called Hypothesis Testing; we refer to the hypothesis that the gene has no effect as the Null Hypothesis, H0, and the hypothesis that the gene in fact does have an effect as the Alternative Hypothesis H1.
What we would like to say now is ‘given that it is very unlikely that healthy mice would get this ill, it is likely that our knockout mice in fact have an abnormal immune system’. And this is where, with a statistical war-cry, the Bayesian objection rounds the hill.
We are trying to make a decision about P(H | E), the probability of H, our hypothesis being true, given E, our evidence. This is given by Bayes’ theorem,
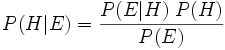 ,
,
which says that the probability of the hypothesis being true, given our evidence, is equal to the probability of our data being true given our hypothesis, times by the probability of our hypothesis being true before we look at the evidence, divided by the probability of seeing our evidence independent of our hypothesis.
In the case of the mouse gene example, we have P(E | H0) the probability of seeing the evidence we do under the Null Hypothesis (given by the Binomial Distribution), and with a bit of work we can figure out P(E | H1), the probability of seeing the evidence under the Alternative Hypothesis, and if we had the probability of the two hypotheses, we could combine them to give the probability of the data. However, this is all for naught if we can’t say, a priori, what the probability of the two hypotheses are. If we can find no justified values for these, or if we aren’t prep aired to write down our subjective suspicions, we are, alas, stuck. We cannot say how likely our hypotheses are given our data.
Waxing Bayesian
Bayes theorem, when applied to inference, makes a claim that translates pretty well into philosophical musing, which I shall now, with your sufferance, subject you to. It goes something like this: There is one method, and one method only, with which we can make inferences about the world. We take our prior beliefs about the world, our priors, and we modify those with evidence. Any attempt to infer something about the probability of a thing being true directly from evidence, without taking into account our prior beliefs, is doomed to failure**.
The Bayesian paradigm says that any system which does not derive probabilities from modification of priors must be an ad hoc system, which sneaks priors in through it’s implicit assumptions, unacknowledged and unexamined. This is aimed very pointedly at the classical school of statistics that formed during the first half of the 20th century, which strove towards objective inference.
I fear that I may have given you the impression that Bayesian statistics is just empty criticism of the classical school. This is very far from the truth; Bayesian statistics has produced some wonderful methods of inference, based on finding good ways to choose priors, and ways of performed the complex calculations required to solve Bayes Theorem for complicated problems. Within my own field of sequence analysis, life has been saved many a time by the Bayesian cavalry, in the form of Bayesian Markov-Chain Monte-Carlo.
There is deep theoretical justifications for the Bayesian perspective, and strong evidence that any approach that is not based on this must be inconsistent (there are instances when it will fail). For an entertaining summary of these arguments, take a look at Why Isn’t Everyone Bayesian?, which also includes a wonderfully snarky response from Dennis Lindley, a major player in Bayesian statistics:
It may be that we Bayesians are poor writers, and certainly the seminal books by Jeffreys and de Finetti are difficult reading, but it took Savage several years to understand what he had done; naturally, it took me longer. The subject is difficult. Some argue that this is a reason for not using it. But it is always harder to adhere to a strict moral code than to indulge in loose living.
As for my opinion on the loose living of classical statistics, I will leave for another time.
Picture and equation from wikipedia.
———————————————————
*this is a toy example, as a gene knockout may cause lots of problems in a mouse even if it doesn’t act directly on the immune system. Perhaps we could use some negative controls, perhaps different mice with genes knocked out that we know aren’t part of the immune system? Perhaps you have some suggestions?
**This does not mean that any inference is determined entirely by our prior beliefs, of course. It is entirely possible to have a situation in which evidence exists that will totally outweighs any priors that you may hold.









Why isn’t everyone a Bayesian? It’s the prior, of course. You have to specify it. This makes a lot of people (myself included) rather uncomfortable. Yes, classical statistics usually involves updating prior beliefs on the basis of evidence, and, unlike in Bayesian statistics, this is done in an ad-hoc and informal manner. But that’s not necessarily a bad thing.
If we aim to devise a formal system for updating beliefs on the basis of evidence, what we end up with is Bayesian statistics, and at that task it works extremely well. But doing this formally requires us to formally specify a prior, and should we use a prior that is in some way inappropriate, the formal chain of reasoning will lead us to an undesirable conclusion. It’s not that hard to do — uniform priors for a binomial success rate, say, or Wishart priors for a covariance matrix, seem sensible but have subtle flaws.
Should we update our beliefs in an ad-hoc and informal way, however, this leaves us free to be guided by our common sense and true prior belief. The statistics is then in some sense objective (no, not truly objective, but perhaps moreso than a Bayesian analysis); readers wishing to produce a subjective judgement from it are free to do so in the privacy of their own heads.
Many Bayesians take issue with the fact that, in classical school, the same data can have different interpretations depending on what you were thinking when you obtained it; you can, for example, bias a test by stopping as soon as you obtain a positive result. This is worrying, yes, but provided you trust the person performing the experiment to use good experimental design, it’s not really an issue. (If you don’t, you shouldn’t be using the data in the first place!)
Furthermore, if we perform inference that respects the likelihood principle, these problems do not arise. Bayesian inference naturally does this, but so do many modern methods: maximum likelihood estimators, generalised linear models, and applications of Wilks’ Theorem generally. Yes, minimum variance unbiased estimators are a bad idea. We know. It doesn’t mean there aren’t any good ideas.
Now, this might give you the impression that I don’t think much of Bayesian stats. On the contrary, I think it’s very powerful, but I think it’s best used in certain situations: there’s an obvious objective prior; there are reasonable subjective priors, and enough data to swamp them; or there’s no good classical test, so we use MCMC and hope for the best. (I gather that last case applies rather a lot.)
Bayesian statistics does allow you to easily deal with situations that in the classical set-up require much more work: sparse inference, multiple testing and meta-analysis are trivial within the Bayesian school, but each requires an individual, ad-hoc method in classical statistics. More worryingly, the classical hypothesis test is not even consistent! (I mean this in the technical sense that it does not, given infinite data, always produce the correct answer.)
But this is the price we pay for being unwilling to quantify our beliefs about the world. We cannot average over all possible worlds; we must devise techniques that work in this one, whatever that may be. Whether you think it’s worth it depends on how comfortable you are with specifying a prior.
A much less intellectual comment than above: The mouse is adorable!
I certainly hadn’t realised that the further you get into Maths it starts to blur with Philosophy.